
|
- Read claims in books and online about the golden ratio
and assess which you can justify as valid.
|

|
- Make a hyperboloid using shish-ka-bob skewers and
rubber bands.
- Make a hyperboloid that can twist, using two disks and
string.
- Make one large enough to walk through.
|

|
Long
Sword Dancing
- Invent some popsicle-stick bombs.
- Can you give rules that predict when they are
stable?
- Using yard-sticks (or meter-sticks) try the dances
shown.
|

|
- Try it!
- Experiment with varying materials to better understand
the process.
|
|
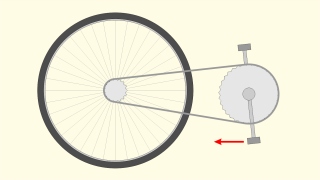
- Challenge your friends to predict what will happen
with their bicycle, then try it.
- Challenge your friends to predict what will happen
when you pull the thread on a spool as shown (or pull
the string of a yo-yo) and then try it.
|

|
- Play all the permutations of three, four, then five
notes on a piano or other instrument.
- Work in a group of n people, each with a sound
or word, to produce all n! permutations.
- Work in a group of n people to do the n-person
"dance" that shows all n! permutations.
|

|
|
|
- Experiment with the free ChordGeometries software
available here
for visualizing spaces of musical chords.
|
|
- Examine the dimple patterns on different brands of
golf balls.
- Make paper models of the first half dozen
possibilities.
- Read the paper cited with the video and solve the open
problems about "paths."
|

|
Juggling
- Learn to juggle and learn about "site-swap
notation."
- Understand Shannon's Juggling theorem.
|
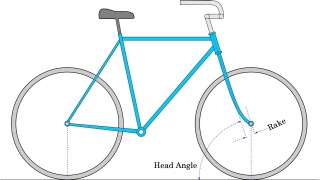
|
- Look for real bicycle tracks and figure out which way
the bicycle went.
- Consider whether a bicycle can make a single track,
like a unicycle, other than the special case of a
perfectly straight track. Then look up the paper Can
a bicycle construct a unicycle track? by David
Finn.
|
|
- For each 3D symmetry group, make a list of the things
you find around you that have that symmetry.
- Construct your own "sculpture" for each 3D symmetry
group.
|

|
- Calculate the angle you expect to find between faces
of an octahedron, rhombic dodecahedron, or
pyritohedron.
- Obtain some of the crystals shown, measure their
dihedral angles, and compare them to what you expect.
|

|
- Cut a
bagel, an inner tube, or other toroidal object to
form a trefoil (in two fundamentally different ways).
- Read about torus knots and see what other ones you can
make physically.
|
 |
- Cut a cube of potato or cheese to reveal a regular
hexagonal cross section.
- Combine 20 cubes of wood, foam, or something, to make
a 1st-order approximation to the Menger Sponge and slice
it to reveal its special cross section.
- Learn about a 3D modeling program (e.g., Blender or
OpenScad) or ray tracing program (e.g., PovRay) to
generate your own models and see their cross sections.
|
 |
- Use the software shown to generate some algebraic
surfaces or Seifert surfaces.
- Explore Mathematica, Maple, or other software that can
make other families of mathematical models
- Find a local 3D printer or use an online 3D printing
service bureau to physically produce your models.
|
 |
- Make the two paper
models shown: four triangles and six squares.
- Make the regular polylink of six pentagons from paper.
- Explore other materials for making polylinks, e.g.,
wood or basketry.
|
 |
- Simulate some of the rules shown, using two colors of
checkers, beads, etc.
- Invent your own rules and see what patterns they lead
to.
- Write a program which can follow your rules more
quickly and accurately than you can.
- Examine real shells (or online photos) and classify
their pattern by which rule generates them.
|
 |
- Make a large geometric construction using one of the
templates here: (1),
(2),
(3).
- Design your own giant mathematical object to build.
|













