George W. Hart's Millennium Bookball is a geometric sculpture, five feet in diameter, commissioned by the Northport (New York) Public Library. The work is a spherical assemblage of sixty wooden "books," and bronze connecting elements, hanging in the library's two-story main reading room. Its structure is based on the geometry of the rhombic triacontahedron, with components rotated to generate visually interesting internal coherences. The books are made of various hard woods, with the titles and authors of "the best books of the century" carved and gold leafed. These titles were voted on by library patrons, and the sculpture was assembled at a community assembly event, like a barn raising, but for art. Dedicated on December 12, 1999, it is on permanent display, celebrating great books and geometry.

As a sculptor of constructive geometric forms, my work deals with patterns and relationships derived from classical ideals of balance and symmetry. I use a variety of media, including paper, wood, plastic, metal, and assemblages of common household objects. Mathematical yet organic, I try to create abstract forms that dance with motion, inviting the viewer to partake of the geometric aesthetic. [1-5]
 

Figure 1. Millennium Bookball

In October, 1998, I wrote a proposal to the New York State Council for the Arts, (NYSCA) requesting a grant to produce the Millennium Bookball as a community art project. The sculpture would celebrate the best books of the millennium. The proposal also explained that I was interested in the geometry, materials, design, and other sculptural aspects of the form, but was not concerned about the exact titles of the books, so a community vote would select the titles.

A key aspect of the design is that one person alone, or even a small group of people, could not assemble the sculpture. Many people had to hold a large number of components together in their relative positions, and slide them together simultaneously. The sculpture embodies the idea that art needs a community to support it, in this case not just monetarily, but for its very existence.

The proposal was funded by NYSCA with an individual artist's award, administered through the Huntington Arts Council. I approached the Northport Public Library for co-funding and a permanent site. Their management and board of directors enthusiastically supported the idea and it was agreed that the library would organize a community fund-raiser to support a large-scale permanent sculpture that was more substantial than my original proposal. The library created voting booths, (allowing three write-in votes per patron) arranged publicity, contracted for a hook in the ceiling, and took care of all other matters, allowing me to focus on the fun part, sculpture.

In my sculpture, I seek to create forms that are enriched by an underlying mathematical depth. While viewers sometimes describe my works as spheres, I see them not as spheres, but on spheres. One would not say that oil painters traditionally paint rectangles, but they paint on rectangles. So, I see the sphere as a canvas to sculpt upon. From the design perspective, a sphere presents a significant challenge, because there is no convenient edge to the canvas. The form must meet with itself "around the back" in a coherent manner—and every side is the back.

I mainly design by visualization, but also use paper and computer models [5-6]. Like most of my work, this piece went through many design iterations. For illustration, three significant stages in the evolution of the Millennium Bookball are presented here.

In my initial design, there are sixty directly interlocking books. The books are each identical, with five slots cut in each. Figure 2 shows the paper model that I presented with the proposal. The figure does not make clear its subtle coloring pattern: there are ten books in each of six different colors, with each book's five neighbors being of the other five colors. Figure 3 is the template for each book. If you make sixty photocopies of the template onto colored card stock, cut them out, slit the slits, and slide them together, you will duplicate my activities on the night before the proposal was due.
 

Figure 2. Initial design	Figure 3. Book template

Part of what is visually interesting about the form in Figure 2 is that it is not immediately clear to the casual observer that the books are identical. Because of their many different orientations, this strong relationship between the components is only noticed on longer viewing. Some viewers of the paper prototype expressed a feeling that it is impossible to make a "jigsaw puzzle" like that where all the pieces are identical.

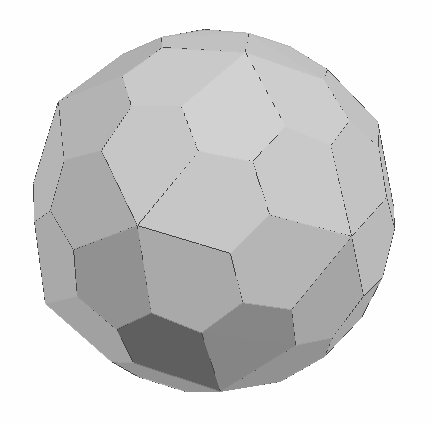
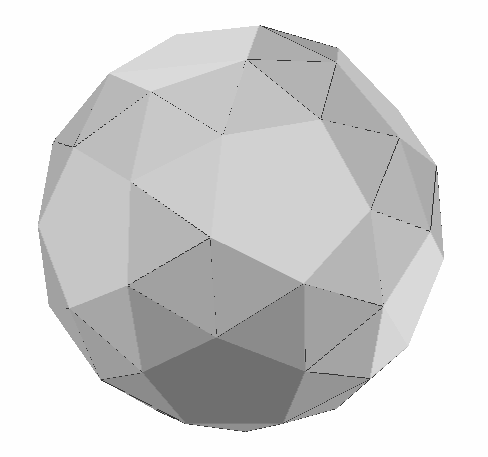
To understand the structure behind the form in Figure 2, it helps to be familiar with the polyhedron known as the pentagonal hexecontahedron, Figure 4. The most familiar variant of this polyhedron is the dual to the Archimedean snub dodecahedron. The snub dodecahedron, Figure 5, is composed of 12 regular pentagons and 80 equilateral triangles. There are sixty identical vertices, each incident to one pentagon and four triangles. This form was presumably known to Archimedes, though his text concerning it is lost, and was rediscovered around 1600 by the astronomer and mathematician Johannes Kepler [7]. The French mathematician Eugene Catalan discovered its dual, the pentagonal hexecontahedron of Figure 4, in 1865 [8].

Fig. 4 Pentagonal hexecontahedron	Fig. 5. Snub dodecahedron

This hexecontahedron can be derived by imagining the snub dodecahedron inscribed in a sphere. Where each vertex touches the sphere, a tangent plane can be constructed, and the region interior to all sixty planes is the hexecontahedron. Because the sixty vertices of the snub dodecahedron are identical, the sixty faces of the hexecontahedron are identical. Because the vertices of the snub dodecahedron each connect to five neighbors, the faces of the hexecontahedron each have five sides. Because the snub dodecahedron has edges of a single length, this hexecontahedron has all its dihedral angles equal.

To go from the polyhedron of Fig 4 to the template of Fig. 3, it is just necessary to make a drawing of one face and overlay it with a rectangle. Imagine sixty books, one on each face, extending slightly beyond each face. Where they cross each other, the books have slits.
 

Fig. 6. Mobius triangles

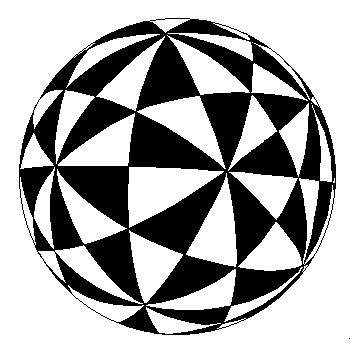
It is not generally appreciated that there is an infinite number (a two parameter family) of geometrically distinct polyhedra like Figure 4, with the same connectivity and symmetry, and each having sixty identical pentagonal faces. They can be derived starting from the sphere divided into 120 Mobius triangles, Figure 6. Each triangle corresponds to one tenth of a dodecahedron face or, equivalently, one sixth of an icosahedron face. Black and white indicates left and right-hand triangles. Pick any point inside one of the sixty white triangles, and then mark the corresponding point in the other fifty-nine white triangles. The region interior to the sixty tangent planes at these points will be a pentagonal hexecontahedron. Figure 4 corresponds to a special choice of initial point—the snub dodecahedron vertex—giving a "canonical polyhedron." [9] By adjusting the initial point within this triangle, many other pentagon shapes are possible, giving the artist a range of choices. The design in Figure 2 is based upon a different point, chosen by experimentation with an interactive software tool of my own construction.

The initial design, above, was conceived with a pedestal mounting. Although very strong structurally, due to the tight interlocking, it is very closed visually. After learning that I could make a hanging sculpture, I decided that I wanted a more open design, which would have the effect of floating.
 

Figure 7. Second design

Figure 7 is an illustration of an intermediate design, produced by special-purpose software which I wrote using the Mathematica software package. This form keeps the notion of sixty books, and the overall icosahedral symmetry. In effect, each book of the initial design is simply rotated in place, allowing visual access to the interior. The rotations are chosen so each book has edge-contact with two other books, resulting in a rigid structural integrity. This can be fabricated by pre-assembling twenty groups of three books, with one slit per book. The twenty groups can then slide into each other simultaneously and be fastened.

This form strongly suggests a dodecahedron. Although opening access to the interior was a step in the right direction, I found it somewhat chunky and overly simple. I quickly saw what I liked about it, and kept going in the same direction.

My final design involves hollow wooden books connected via bronze hubs. The thirty-two hubs are the "donuts" visible in Figure 1. Casting bronze components was a possibility that arose because of the financial support of the library fundraiser. It makes sculptural sense because the hubs provide a framework in which each book stands on its own, inviolate, un-slit. Structurally, the strength of metal hubs allows for many design options. Although it has a very different visual impact, this structure is actually very similar to the two earlier designs, with each book simply rotated in place into a different orientation from the above.

From hub-to-hub is a structural steel rod passing through the inside of each book, which carries the load. The toroidal hubs were drilled very precisely for the rods and tapped for setscrews, which lock everything together. Twelve of the hubs are 5-fold connectors and twenty are 3-fold.

Figure 8. Rhombic triacontahedron

Although I did not begin with this thought, the final design is based upon the rhombic triacontahedron (RT), Figure 8. This polyhedron consists of thirty equal rhombi and sixty edges. Each edge corresponds to the steel rod through one of the books. In Fig 8, I have rendered the RT with open faces, a style of illustration invented by Leonardo da Vinci. Each face has enough body to give a sense of its planarity, easily distinguishing front surface from back, (avoiding the "Necker cube" effect) yet the openness allows the whole structure to be grasped at a glance.

Figure 9. Kepler's illustration

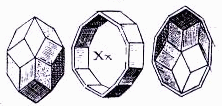
The RT was first described by the astronomer and mathematician Johannes Kepler. [7] (However, it was forgotten and independently rediscovered by Catalan 250 years later. [8]) Figure 9 shows the illustration from Kepler's 1619 book, Harmonice Mundi. While not in accurate perspective, Kepler's illustration highlights a key property of the RT: It can be assembled as an "equator" and two "caps," with ten rhombi in each component. This property is key to understanding the assembly process described below.

Mathematically, the RT is a member of the class of polyhedra called zonohedra, first recognized by the Russian crystallographer, Evgraf Fedorov in the 1890's [10]. These polyhedra have a number of interesting properties. [11] A key characteristic of zonohedra is that their edges are grouped into sets of parallel edges called zones. The RT has six zones of ten edges (or ten faces) each. In each zone, there are ten parallel edges. Kepler's illustration points out one zone. In the sculpture this translates into six sets of ten books; in each set the books' ten spines are parallel.

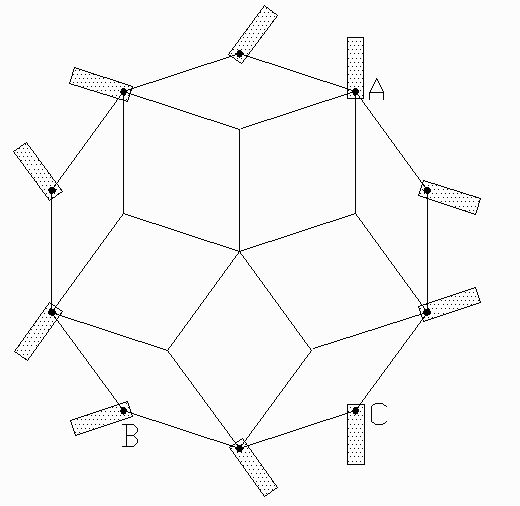
If we look along the direction of an edge, we see the projection of the RT illustrated in Fig. 10. The ten dots represent a zone of ten parallel edges, seen on end. The lines are the edges of one cap of ten rhombi. The rectangles indicate the orientation of ten books. To add visual coherence to the sculpture, each book is rotated about its spine to be coplanar to another book on the opposite side, e.g., books A and C are aligned.
 

Figure 10. End view of ten books.

Figure 10 shows how the appropriate angle is determined. Because the ten rods are spaced 36 degrees apart about the center, O, of the circle, angle BOC is 72 degrees. BAC is half that because the angle seen by a point on the circumference is half the angle seen at the center. So each book is rotated 36 degrees from a radially outward, alternately left and right.

To fix this 36 degree rotation angle, there is a steel bracket inside each book, screwed to the wooden interior. The bracket was brazed to its rod in a fixture that accurately set its position relative to two flats milled near the ends of the rods. The flats are locked by the setscrews in the bronze connectors.
 

Figure 11. View along 5-fold axis.

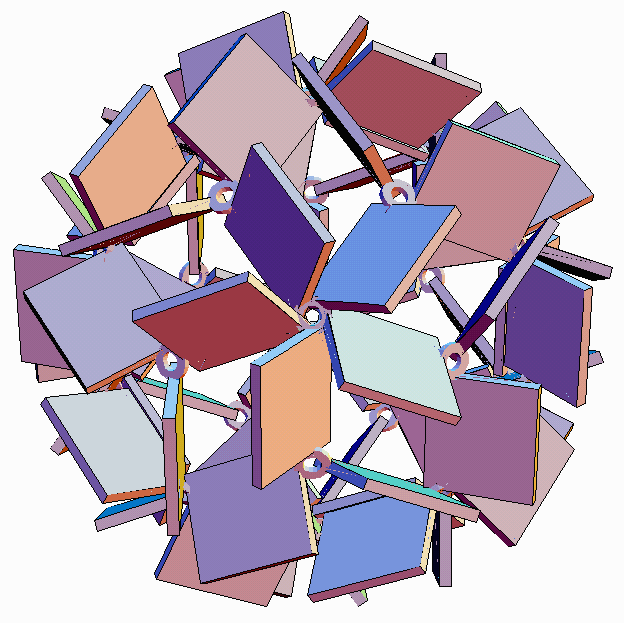There are several natural ways that the books could have been colored with a six-color or a five-color pattern. To choose among them, I made several paper models before selecting the final six-color pattern. Each set of ten books is constructed from a different hard wood. The six woods are maple, cherry, sapele, bubinga, purpleheart, and walnut. The effect of this arrangement is that at each 5-fold meeting point, a combination of five different woods meet to form a "propeller." At each 3-fold meeting point, three different woods make a "propeller" which spins in the other direction. Each book connects a 5-way and a 3-way connector, and appears to spin clockwise in one yet counterclockwise in the other.

This sculpture can not be assembled by a single person. One might begin easily enough. But at the time for placing the final piece, there would be no way to insert it, as both ends of its rod would have to slide into connectors. However, with a large group of people, this problem can be circumvented.
 

Figure 12. Books at start of Assembly	Figure 13. Initial Connections

The geometry of the zonohedron suggests the method for its assembly. It is easiest to understand the assembly in reverse sequence. Imagine taking the sculpture apart, referring to Kepler's Fig. 9. Because the cap of ten rhombi fits on to ten parallel edges, the final step in the assembly is to join the cap of ten rhombi onto the cap-plus-equator structure. Ten connections—ten rods into ten donuts—must be made simultaneously. This required ten people to guide the junction, ensuring that the penetration was uniform and nothing jammed at an angle. Previously to this, the cap had to be assembled, by making a connection of five simultaneous joints analogously. The subparts of the caps were similarly built up by simultaneous parallel connections.

The Northport Public Library arranged for a community sculpture-raising event at which this occurred. See Figures 12-15. Dozens of volunteers came and worked together for the two hours that it took. Although I was somewhat nervous that someone might drop, scrape, scratch, or otherwise damage components, everything went very smoothly.
 

Figure 14. Half-way done	Figure 15. Final connection of ten struts

Two months previously, the library had arranged a title-announcement party, at which the winning books were unveiled in a countdown from number sixty up to number one. The title voted number one is The Catcher in the Rye; the complete list can be found in [1]. In the intervening months, I had carved all the titles and authors into the covers with a computer-controlled router, and gold-leafed them. For the assembly, we only had to connect everything in the proper positions and tighten the 120 setscrews. As a construction guide, I brought along a small Zometool model of the rhombic triacontahedron, [12] with colored paper indicating the positions of the books.

The Millennium Bookball is now suspended by chain from one of the 5-fold connectors. Weighing 160 pounds, raising it was straightforward with a block and tackle. It is set near a balcony so it can be seen from its own height or from below. All the titles are visible from somewhere, but if one seeks a particular title, it may not be obvious. In order that viewers might easily find their favorite books, I positioned the books in numerical sequence in groups of ten. The books voted 1-10 are placed in order in the walnut equator, the darkest wood. Books 11-20 are in order in the purpleheart equator, a slightly lighter wood. And so on up to 51-60, in maple, which is the lightest. So looking up any title in the brochure which the library provides, one can determine its number and the wood of the equator it in which to find it. Then examining whatever books one sees in that wood, finding their numbers on the list, one can count around the sculpture to the desired book.

The Millennium Bookball is a sculptural celebration of great books and geometry. It is a community artwork in three ways: the "best books of the century" titles were selected by vote, a fundraiser supported it financially, and it was physically assembled at a "barn raising." I feel the geometric basis of its form gives it a depth, so viewers discover more and more of its properties over time, while it also serves to instill an appreciation for mathematics.

For more images of the sculpture and its assembly, a list of the sixty titles, press clippings, acknowledgments of many who helped, and other examples of my geometric sculpture, see [1].
 

Figure 16. View along 3-fold axis (compare to Fig.1)