Renaissance Banff:
Bridges + Coxeter Day
Banff, Alberta, July 31-August
3, 2005
Orderly Tangles Revisited
Computer Science Department
Stony Brook University
Stony
Abstract
In the 1970s and 1980s Alan Holden described
symmetric
arrangements of linked polygons which he called regular
polylinks and constructed many cardboard and stick models.
The fundamental geometric idea of symmetrically rotating and
translating the
faces of a Platonic solid is applicable to both sculpture and puzzles.
The insight
has been independently discovered or adapted by others, but the concept
has not
been widely used because no closed-form method is known for calculating
the
dimensions of snugly fitting parts. This paper describes a software
tool for
the design and visualization of these forms that allows the dimensions
to be
determined. The software also outputs geometry description files for
solid
freeform fabrication, and image files for printing and cutting out
paper
templates. The paper templates make it easy to teach the concepts in a
hands-on
manner. Examples and variations are presented in the form of computer
images,
paper, wood, and solid freeform fabrication models.
1. Introduction
Figures
1 and 2 illustrate the key ideas of Holden’s regular
polylinks [5] [6] [7]. The six hollow faces of the inner
cube are separated, translated radially outwards from the center, and
each
rotated the same angle clockwise about their center. In Figure 2, the
original
cube is removed, the faces are moved inward until they interweave, the
rotation
angle is adjusted slightly, the thickness of each plane is reduced to
paper-thinness,
and the size of each square hole is shrunk slightly to make a snug fit.
Each
square links with four others. From the underlying cube’s symmetry, the
rotational axes are preserved but not the mirror planes.
 |
 |
 |
| Figure 1. Rotation and translation of cube faces | Figure 2. Regular polylink with six squares. | Figure 3. Paper model of six linked squares. |
It
is instructive to create a paper model of Figure 2 by cutting out six
hollow
squares and interweaving them. Four of the squares can be cut open,
linked
through the other two, and then taped together. Figure 3 is a photo of
a model
made using three colors of card stock, iso-coloring
parallel
faces. It is chiral so one must choose between two
enantiomorphs. The
only critical parameter is the ratio of the edge length of the outer
square to
the inner square hole. By means of the software described below, a
ratio of approximately
15/11 is determined to be suitable. So the outer square can be 3.7
inches on
edge with a 2.7-inch square hole, leaving 0.5 inch of solidity on four
sides,
and four fit within an 8.5 by 11 inch sheet. This is easily drafted and
cut out
from paper. Or simply make six enlarged photocopies of Figure 4. For
even
larger models, use cardboard. Figure 5 has the same weaving as Figure
3, but
the strut cross section is made into squares, to give it enough
internal
substance to hold together when fabricated as a solid freeform
fabrication
model. This fused deposition model (FDM) is 2.5 inches in diameter.
 |
 |
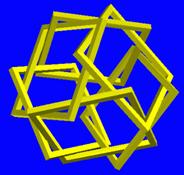 |
| Figure 4. Hollow square template for making model in Figure 3. | Figure 5. FDM model with square strut cross sections. | Figure 6. A different weaving of six squares, also based on cube. |
Holden’s
regular polylinks are the topologically distinct polygon linkages that
result
from varying the rotation and radial translation starting with the
faces of any
of the five Platonic solids. There can be several distinct ways of
linking the
rotated faces from any underlying polyhedron. Figure 6 shows a second
way of
linking six squares, but they still lie in the face planes of an
imagined cube.
Starting from a dodecahedron, one regular polylink of twelve pentagons
is shown
in Figure 7.
The
struts which form the polygon edges in Figures 1-3
have rectangular cross-sections, and in Figures 5-7 they have square
cross
sections. Holden made his models using ¼-inch diameter wooden dowels of
circular cross section. The critical dimension for a snug fit is the
ratio of
the strut length to diameter. He experimented until he found the
shortest lengths
that could be assembled, and gave a table of his results for others who
replicate the constructions with round dowels [7]. But different
dimension
ratios are needed if one prefers square, rectangular, or other cross
sections.
 |
 |
 |
| Figure 7. Regular polylink with twelve pentagons. | Figure 8. Regular polylink with six pentagons. | Figure 9. Paper model of Fig. 8. |
Figure
8 illustrates a special case to consider. The faces of a dodecahedron
are
translated in to a distance of zero from the center. Then by proper
choice of
rotation angle, it is possible to cause opposite faces of the
polyhedron to
coincide. So the twelve faces of the dodecahedron fuse into six
concentric interwoven
pentagons of figure 8. A paper model of this, Figure 9, is made from
pentagons
of 3-inch edge, having pentagonal holes of 2.5-inch edge. Analogously,
the six
faces of a cube can be translated to the origin where they fuse into
three orthogonal
concentric squares. But because squares have an even number of sides,
they intersect
other squares (in either of two rotations) rather than forming a weave.
With
pentagons or triangles a non-self-intersecting polylink can be formed.
 |
 |
 |
| Figure 10. Regular polylink composed of four triangles. | Figure 11. Paper 5-inch triangles, 2.5-inch holes, seen on 3-fold axis. | Figure 12. Three nested regular polylinks, each like Figure 8. |
The
symmetric intricacy attainable with simple components makes polylinks
very
appealing aesthetically. Holden illustrates only small cardboard models
and
dowel models, but he suggests their use in “constructivist sculpture”.
I have
run into a dozen or so examples of sculptures based on his suggestion
or a
rediscovery of the essential ideas, and there are many ways to adapt,
combine,
or extend them. For example, Robert Lang, George Odom, Rinus
Roelofs, and Carlo Sequin have explored the
minimalist
construction of four triangles shown in Figure 10 [1, 8, 9, 10, 11]. It can be derived from either the
tetrahedron or the
octahedron by translating the triangles in to the origin. Deriving
Figure 10
from a tetrahedron shows that a degree of rotational freedom remains.
Starting
from the octahedron explains its axis of 4-fold symmetry; a particular
rotation
angle causes faces to merge in pairs. Coxeter analyzed this
construction and
showed: (1) if made of zero-thickness material, the hole in each
triangle has
exactly half the edge length of the whole triangle, and (2) the twelve
outer
vertices lie at the midpoints of a cube’s edges, i.e., the vertices of
an
Archimedean cuboctahedron [2]. I recommend the reader make a paper
model, as in
Figure 11.
A
very large polylink sculpture is Charles Perry’s 1976, twelve ton “Da Vinci”, based on the six-pentagon polylink of
Figure 9. See
[3], plate D for a figure. Perry made flat steel pentagons 20-feet on a
side,
and nested two copies of the construction together. Figure 12
illustrates this
idea but takes it further to have three concentric copies. The series
can be
extended inward to any depth because the components are progressively
reduced
in size geometrically towards the center.
Holden
does not define orderly tangle
precisely, but uses it loosely to subsume a variety of interesting
forms such
as highway interchanges, woven cloth, and polylinks. A form such as
Figure 12
is not a regular polylink (because it is three regular polylinks) but
it fits
under the broader heading of orderly tangle.
2. Puzzles
A wooden
puzzle based on the twelve pentagons of Figure 7 is shown in Figure 13.
In
Figure 14 is a wooden puzzle made of 30 identical sticks, which form
ten
triangles. It is based on an icosahedron, with the 20 faces translated
to the
center and rotated to coincide into ten pairs. In both puzzles, the
square
wooden sticks are cut longer than the polygon edges, and are notched to
lock
together gluelessly with half lap joints.
I received
these beautiful works as presents during a trip to
 |
 |
| Figure 13. Wooden puzzle by Lin and Wu. | Figure 14. Wooden puzzle by Lin and Wu. |
This
puzzle idea of Lin and Wu can be applied to many other polylinks if one
can
determine the proper length to cut the wooden sticks. As a simple
example, the
polylink shown in Figure 5 can be built from square stock if the ratio
of the outer
edge to the cross-section edge is 9.8 to 1. This value comes from the
software
described in the next section, but as wood is flexible and
compressible, some
experimenting was still required. So from 1-unit square stock, one can
cut 24
pieces, each 11.8 units long. Near each end, but from opposite sides,
notch
halfway through to leave a 1-unit overhang beyond the notch. Figure 15
shows
the assembled result. Figure 16 is the analogous puzzle of thirty
sticks
assembled into six pentagons woven as in Figure 8. I built both of
0.5-inch
square wood bars.
 |
 |
| Figure 15. Puzzle based on Figures 3 and 5 | Figure 16. Puzzle based on Figure 8 |
In
these two experiments, I found that cutting the lengths a few percent
shorter
than the software suggests seems to compensate for the flexibility of
the
struts and the fact that the corners of wood struts may be compressed.
So
although the software provides a good initial value, the woodworker is
advised
to plan on some experimentation with scrap wood before investing in
quality
wood.
3. Software
To
design and build regular polylinks and tangles of concentric polylinks,
I wrote
a program with sliders that can be adjusted to see a wide range of
structures
on-screen. The computer-generated images in this paper are from
screen-shots of
its operation. The user can specify any number of polylinks to be
assembled
concentrically, and for each set, the user selects the underlying
polyhedron used
as its basis. Then sliders allow the size, translation, and rotation of
the
components to be adjusted. At present, the edge cross sections are
adjustable rectangles,
allowing flat (paper) versions as the special case of width zero. As
the
sliders are adjusted, the dimensions of length, width, thickness, etc.
are
displayed, which can be used for making models of wood or other
materials. When
the user is happy with the form shown rotating on the screen, a click
of a
button generates an STL file for making solid freeform fabrication
models,
e.g., Figure 5. Clicking another button generates an image file that
can be printed
for making paper or cardboard models, e.g., Figure 4.
Three
4-cm examples made by selective laser sintering (SLS) from the
program’s STL
output are shown below. Figures 17 is ten triangles, arranged as in
Figure 14,
but with a “tall” cross-section. Figure 18 is twenty icosahedrally
arranged triangles, with the minimum possible linkage (analogous to the
cubic
form in Figure 6). Figure 19 is a weave based on the octahedron but
with the triangles
replaced by hexagons.
|
|
|
|
| Figure 17. 10 triangle SLS model, based on icosahedron. |
Figure 18. 20 triangle SLS model, based on icosahedron. | Figure 19. 8 hexagon SLS model, based on octahedron. |
The
software is freely available online at my website [4]. It has only been
tested
on PCs, but it is written in java so should be transportable to other
computing
environments. For rendering 3D images on the screen, it uses Sun’s
freely
available java3D extension, which must
be installed on the user’s computer. The coding is quite
straightforward, with
no clever algorithms or data structures needed. I believe it can be
straightforwardly
replicated by any software engineer with expertise in graphics
programming.
Users
may verify their understanding of its capabilities by replicating the
figures
of this paper, or one can simply start playing to create new objects.
The
software generates all regular polylinks including several icosahedral
examples
that Holden did not describe. Lang enumerated the regular polylinks
with a
computer search and showed there are 2
tetrahedral, 2
cubic, 3 octahedral, 5 dodecahedral, and 23 icosa-hedral
varieties (excluding the extreme cases where polygons either are not
linked or
are merged into pairs) [8]. I can replicate these numbers with an
independent
geometric technique of counting subsets of symmetry axes that pierce
the
interior of a polygon centrally placed in the stellation
diagram.
Many
extensions of the program are possible. It could be straightforwardly
modified
to produce circular, triangular, or other shapes of cross sections for
the
polygon edges. Another possible addition to the software is a numerical
search
for slider settings that result in a snug fit. I planned for this
feature when
originally designing the software, but then discovered that it is
simple to see
on the screen if there are gaps or overlaps in the components, so
manual adjustment
seems sufficient.
4. Variations
There
are an unlimited number of variations on the above ideas. For example,
Holden
made several models of linked polygonal stars instead of convex
polygons.
Similarly, one might try rectangles or rhombs instead of regular
polygons; I have
not implemented any of these with software. (For related rectangle
linkages,
see [11].) Another idea is to start with polyhedra other than the
Platonic
solids. Holden constructed examples based on Archimedean solids, e.g.,
the
rhombicuboctahedron and the snub cube. One can symmetrically combine
multiple
polylinks based on different polyhedra; sets with the same symmetry
combine to
form a tangle with the same symmetry. Figure 20 shows the combination
of a
cubical and a tetrahedral form. It combines the tangles of Figure 2 and
Figure
10 so each triangle links three squares while each square links two
triangles.
Figure 21 shows the union of a dodecahedral and an icosahedral form in
which both
puzzles of Figures 13 and 14 are intertwined.
 |
 |
| Figure 20. 6 squares plus 4 triangles. | Figure 21. 12 pentagons plus 10 triangles. |
Another
variation Holden tried was to put squares around the twelve 2-fold axes
of a
cube, i.e., in the planes of a rhombic dodecahedron. Here the squares
only
exhibit 2-fold symmetry, so their edges and vertices are not all
equivalent,
and the polylink is not regular. I find the results less attractive—fun
to
generate with the software but less interesting to look at. An example
is shown
in Figure 22. Here the twelve squares are grouped together as the sides
of four
triangular prisms. Extending his idea, it is natural to try putting
thirty
squares around the 2-fold axes of an icosahedron, i.e., in the planes
of a
rhombic triacontahedron. These can be
grouped in many
interesting ways, including five cubes or six pentagonal prisms. In
Figure 23,
the thirty squares are grouped together as the sides of ten triangular
prisms.
(When brought to the origin and fused into fifteen squares, they form
five
octahedra.)
 |
 |
| Figure 22. 12 squares, in four triangular prisms | Figure 23. 30 squares in ten triangular prisms |
 |
 |
 |
| Figure 24. Ten sets of squares: inner cube, outer cuboctahedron. | Figure 25. Set of triangles join opposite faces of stella octangula. | Figure 26. Sets of triangles join opposite faces of icosahedron. |
Weaving is another way to generate variations on a polylink. The oldest example that I know of a form closely related to a regular polylink is the sepaktakraw ball, seen in Figure 27. Traditionally woven from rattan, it exhibits the dodecahedral pattern of figure 8. The design goes back centuries for use in traditional Asian “football” games. Figure 28 shows a “spherical basket” I wove of paper strips. The six dark central bands follow the same weave pattern of six pentagons shown in Figure 8. Neighboring bands, which get progressively lighter in color, simply alternate over and under in the natural weave pattern. Note the difference between this weave and the sepaktakraw ball. In Figure 28 the individual strands weave, while in Figure 27 the group of strands weaves as a whole.
 |
 |
 |
| Figure 27. Sepaktakraw ball | Figure 28. Paper weave. | Figure 29. Skew holes. |
Another
variation, illustrated in Figure 29, is to allow a parameter for a
relative
rotation between the polygon and its hole. This adds a dynamic visual
quality
to the forms.
A different type of variation is to replace the straight edges of the polygons with curved paths. There are infinitely many ways to choose curves, but a particularly natural one is to perform an inversion about the center of symmetry. Central inversion replaces each point at distance r from the origin with a point in the same direction but at distance 1/r. This transformation is well studied mathematically but little used in sculpture [12]. In this context, the chain of n rectangular struts that form the edges of an n-gon is replaced by a chain of n curved volumes bounded by four portions of spheres. Figure 30 shows an example in which a square-cross-section version of the four-triangle construction in Figure 10 is inverted into a structure that resembles four interlocked three-leaf clovers. The twelve corners are now on the inside, but remain 60-degree angles because central inversion is an angle-preserving transformation.
 |
 |
 |
| Figure 30. Inversion of four triangles. | Figure 31. Five tetrahedra, an icosahedral polylink. | Figure 32. Inversion of five tetrahedra. |
Figure
31 is the well-known compound of five regular tetrahedra, which is
easily
generated as an icosahedral polylink. It is formed here with struts of
rectangular cross section that overlap to make ribbed edges. These
invert into
the labial forms of Figure 32. The interior regions of Figures 30 and
32 are
very interesting spaces, difficult to capture in a still image.
5. Conclusion
Regular
polylinks are a rich source of fundamental forms that may be used as
the basis
for a gamut of 3D design ideas. Alan Holden’s 1983 book abounds with
creative inspirations
displaying their symmetric elegance. But the spectrum of examples
presented
there and expanded upon here only scratch the surface. To introduce
polylinks
in a concrete manner, paper constructions such as Figures 3, 9, and 11
make a
good hands-on activity. After that, I hope that the polylink-generation
software described here will enable readers to explore new
possibilities.
References
[1]
H.
Burgiel, D.S. Franzblau,
and
K.R.
Gutschera, "The Mystery of the Linked
Triangles," Mathematics Magazine,
v. 69 (1996) 94-102.
[2] H.S.M. Coxeter, "Symmetric Combinations of Three or Four Hollow Triangles," Math. Intel. 16 (1994) 25-30.
[3] Michele Emmer (editor), The Visual Mind, MIT, 1993.
[4]
George
W. Hart, http://www.georgehart.com
[5]
Alan
Holden, Shapes, Spaces and
Symmetry, Columbia Univ. Pr, 1971, (Dover reprint, 1991).
[6]
Alan
Holden, “Regular Polylinks,”
Structural
Topology, No. 4, 1980, pp.
41-45.
[7] Alan Holden, Orderly Tangles: Cloverleafs, Gordian Knots, and Regular Polylinks,
[8] Robert J. Lang, “Polypolyhedra in Origami” in Thomas Hull (ed.) Origami 3, A.K. Peters, 2002.
[9]
Rinus Roelofs,
http://www.rinusroelofs.nl
[10]
Doris
Schattschneider, “Coxeter and the
Artists: two-way inspiration”, in The Coxeter Legacy—Reflections and Projections,
(ed. C. Davis and E.W. Ellers), Fields
Inst. Comm.
v.46, Amer. Math. Soc., 2005. (to
appear)
[11] Carlo Sequin, "Analogies from 2D to 3D, Exercises in Disciplined Creativity," Proc. of Bridges: Mathematical Connections in Art, Music, and Science, Winfield KS, Aug, 1999, and in Visual Math., v. 3, no. 1.
[12]
John
Sharp, “Two Perspectives on Inversion”, Meeting
Alhambra, Barrallo et al. (ed), 2003.
Acknowledgments: Thank
you RJT Educational Training (www.rjtedu.com)
for
making
the model of Figure 5, and thank you Jim Quinn for making the
models of
Figures 17-19.
Addendum: On Coxeter day at the Renaissance Banff conference, when I presented this paper, I received from Marion Walter a slide she took in 1992 of Coxeter holding the four-triangle tangle. He received this cardboard model from George Odom:

To use it, you must first install Java3D, which is also free.


