Web version from
Proceedings of Bridges 2003,
Sculpture from Symmetrically Arranged Planar Components
George W. Hart
Computer Science Department
Stony Brook University
Stony
E-mail:
george@georgehart.com
Abstract
The extended face planes of symmetric
polyhedra form a
set of interconnected canvases that can be used as the basis for a wide
range
of sculptural forms. A special-purpose software tool is described
which
allows the user to select families of such planes, to draw within them,
to
maintain constraints concerning points lying on their intersections, to
view
and modify the results interactively in real time, and to output the
result for
production either as 3D rapid prototyping or 2D laser-cutting,
etc. A
range of examples demonstrate the versatility of the approach.
1. Introduction
Artists
typically self-impose design constraints, challenging themselves to
explore new
possibilities in a restricted genre. I find myself fascinated by the
sculptural
possibilities inherent in symmetrically arranged intertwined planar
components.
Several of my sculptures are 3D forms assembled from flat parts that
lie in
symmetrically arranged planes. For example, Fig. 1 shows Twisted
Rivers,
|
|
|
|
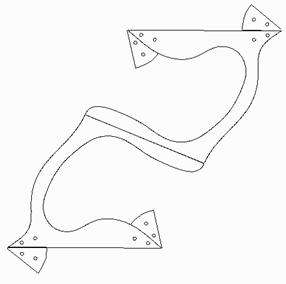
Figure 1:. Twisted Rivers, |
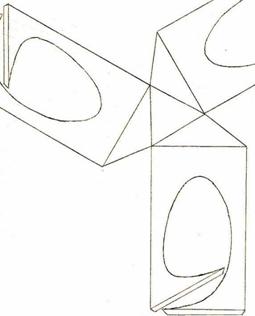
Figure 2: Layout for the 30 components of Fig. 1 |
The sculpture in Figure 1 is assembled from thirty identical curved units. Fig. 2 shows the flat layout for each of the thirty components, before folding the metal. I designed this sculpture by visualization, hand calculation of lengths and angles, and a series of paper models. Then I laid out the flat shape in a standard drawing program and sent the file to a laser-cutting service where the steel was cut on a computer-controlled laser cutter. I folded the parts to the proper angles in a hand brake then sent them out for the blue powder coating. Finally, I wove the thirty parts together and fastened them with stainless steel bolts. Ten pieces meet at each of the twelve junctions where the bolt patterns are visible. The twenty openings are three-fold "whirlpools". If one studies the sculpture in person, it is apparent that groups of three C-shaped curves each lie in a common plane. There are 20 such planes—the planes of an icosahedron.
Figures 3 and 4 show a second example, Fire
and Ice.
This is a 24" diameter hollow form, assembled from sixty identical
pieces
of red oak and ten interwoven loops of brass. These oak components were
also
hand designed using visualization and paper models, and laid out in a
general-purpose drawing program. I then used the file to guide
the
cutting on a computer-controlled router. The two long edges were
then
beveled at 45 degrees, and the short edge at 72 degrees. They fit
together as
they do because the 60 pieces lie by pairs in the 30 planes which are
extensions of the faces of a rhombic triacontahedron.
|
|
|
|
Figure 3:. Fire and Ice, oak and brass, 24"
diam., 1997 |
Figure 4: Layout for 60 wooden parts of Fig. 1 |
Fig
5 shows Whoville, a more complex example in which the planes of
the
sculpture's components lie in the planes of three concentric polyhedra,
an
icosahedron, a dodecahedron, and a rhombic triacontahedron. (At one
type of
joint, along the 5-fold arms, the form incorporates a gradual twist
from one
plane to another, rather than a fold.) This was designed by hand with
the aid
of paper models. For this sculpture, I cut, drilled, and textured
the
metal by hand, then assembled the parts with rivets.
These three examples are members of a rich
family of
possible forms that involve symmetrically arranged planar components.
Only
years after creating these works and others, did I gradually awaken to
the fact
that I could use a special-purpose piece of software to aid me in the
design,
layout, and rapid prototyping of new sculptures in this category.
After
deciding what features I wanted and planning a design general enough
for use in
many new forms, I wrote the program described in the following section.
|
|
|
|
Figure 5:. Whoville, aluminum, 35" diam., 1997 |
Figure 6: Template for paper model of Whoville |
2. A Sculpture Design Program
My
goal in writing this software is to have a tool which can help me
design,
visualize, and produce large sculptures assembled from symmetrically
arranged
flat pieces. The program's editing tools allow me to design and
position
different families of components lying in planes that I specify.
At the
same time, the program shows me a rotating image of the 3D
construction, which
changes instantly in response to my editing any of the planar
components. If I
wish to produce a physical model by stereolithography, fused deposition
modeling, or other 3D rapid prototyping (RP) technique, the program
outputs the
STL file for fabrication. When I have a design finalized, the
metal,
wood, or plastic components can be cut by machinery such as laser
cutters or
water-jet cutters, guided by the 2D layouts the program produces as DXF
files.
The software handles the mechanics of replication, maintenance of
symmetry,
plane intersections, lengths, dihedral angles, and so forth. I can
focus on the
design issues.
Figures 7 and 8 show the
user-interface. As
illustration, Twisted Rivers,
In the background of the editor window, one
sees
"guide lines"—the intersections of this one representative plane with
the other 19 in its family. (This arrangement of lines is known as the
stellation pattern of the icosahedron. [2]. Of the 19 other icosahedral
planes,
only 18 show up as lines, because the plane of the opposite face is
parallel,
so doesn't intersect this face) Over these guide lines, the user can
draw with
the mouse, insert, delete, and move points, connect points with edges,
etc. to
create a 2D layout. Each point can be specified as attached to zero,
one, or
two guidelines. The user's drawing is automatically replicated to
maintain rotational
symmetry in this plane. The toolbar controls the mouse function, and
with
sliders the view can be zoomed, rotated, and panned.
|
|
|
|
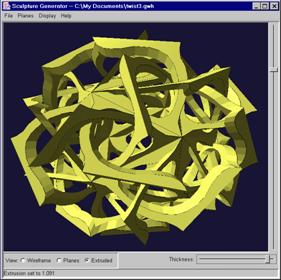
Figure 7:. 3D view window |
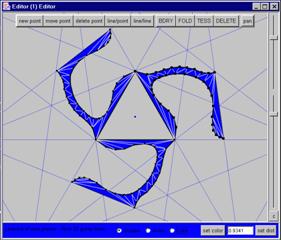
Figure 8: 2D editor window |
In
the 3D window, the user has the choice of three types of view:
wireframe,
planes, or extruded. Fig. 7 is the extruded view, which shows the
sculpture as having a slight (user-specified) thickness, exaggerated
here for
clarity. The 2D pattern is replicated 20 times, in the planes of
an
icosahedron's faces. Each plane is also doubled, to an inner and outer
surface,
connected with a thin edge. At edges where planes meet, the
representation ensures that the surface is "watertight" with no
gaps.
In this form, the model defines a volume, so it can be output as an STL
file
and fabricated by 3D rapid prototyping (RP) machinery. Figure 9 shows a
plastic
model produced from this STL output on a DTM Sinterstation 2500+.
|
|
|
|
Figure 9:. RP model of Twisted Rivers, 9 cm |
Figure 10: Tangled Reindeer, RP, 9 cm |
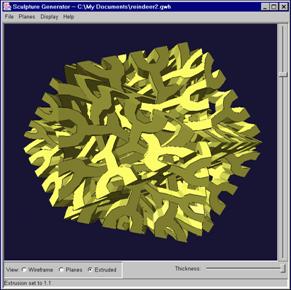
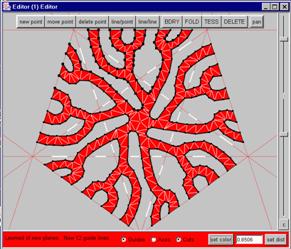
Figure 10 shows a
second RP
result from the program. This is a sculpture titled Tangled
Reindeer,
which is composed of twelve planar components in the planes of a
dodecahedron, though
it nestles nicely inside an icosahedron. The corresponding 3D window is
shown
in Figure 11, and the plan for each plane is shown in the editor window
of
Figure 12. (The background guide lines are now the stellation
pattern of
the dodecahedron.) The white segments in the editor are the
places where
the replicated structures in the other planes pass through this
plane.
The editor optionally shows these cut-through locations, so that one
can see if
the replicated parts will intersect each other.
|
|
|
|
Figure 11:. Tangled Reindeer, 3D view |
Figure 12: 2D pattern in one dodecahedral plane |
The
technical details of the software are beyond the scope of this paper,
but an
outline is as follows. Points are represented standardly as
floating-point
(x,y,z) coordinates, planes as normal vectors and distances, segments
as pairs
of points, etc. There are four types of points: "free-points" are
bound to a single plane and so are draggable in two dimensions,
"line-points" are bound to two planes and so are constrained to their
line of intersection, "corner-points" are fixed to the intersection
of three planes, and "center-points" are fixed at the center of
their plane. There are three types of segments: "boundary
segments", "fold lines" which lie in the intersection of two
planes, and interior "tessellation segments" which simply divide
polygonal regions into triangles because that is required for the STL
file
format. Symmetry and consistency are maintained, e.g., after a set of
planes is
created, the user can change their distance from the origin and points
on those
planes are projected to the new planes, points on the lines of
intersection are
projected to the new lines of intersection, and the guidelines on the
editor
windows move correspondingly.
At present, the extrusion process for
producing STL
files is simply radial in three dimensions from the origin. The
outer
vertices and outer surfaces are generated a few percent further from
the origin
than the inner surface. A slider in the 3D window controls this
percentage, which is 9%–10% in Figures 7 and 11. When extruding,
the
handedness of one set of triangles is reversed to maintain orientation,
and an
edge surface is created by generating a new pair of triangles for each
boundary
segment. This procedure has the advantages of being simple and
preserving
planarity. However it is inadequate in certain cases (not shown
in this
paper) when there are two families of planes of different distances and
the
outer surface of one meets the inner surface of the other. It also has
the
limitation that different families of planes are extruded to different
thicknesses. The further a plane is from the origin, the thicker its
extruded
version. However, this is not a fatal fault for a model intended
as a
prototype of the actual sculpture. More general extrusion processes
without
these limitations are planned for a future version of the software.
In Figures 8 and 12, only a few points
approximate
each curve, so the polygonal nature of the curves can be seen
easily. For
production, a more refined curve with many points could be drawn.
Instead, I take the program's 2D file output and convert it from a
segment
representation to a curve representation (cubic splines) in a standard
drawing
program. This second stage of the layout process is beyond the
scope of
this design program. In this second stage, tabs and bolt holes
might also
be added, as seen in Figure 2. Furthermore, the components might be
reorganized, again illustrated in Figure 2, where components from two
different
planes are joined into one piece, which is folded after cutting.
(The
bisecting fold lines are the outermost parts seen in Figure 1. An
alternative
would be to have a joining mechanism, e.g., bolts, along these outer
seams, but
I did not consider that visually appropriate.) Such aspects of the
design are
not within the scope of the program at this time, because the best
choice for
physically grouping components, e.g., tabs, folds, welds, bolts, etc.,
are
individual to each sculpture.
The software is coded in Java, with OpenGL
for the 3D graphics window. (At present there is no standard
binding for
using OpenGL with Java. I chose the GL4Java
binding, which
appears to be popular and stable.) I have been running the program on a
PC under
Windows, but as it is written in Java, it should be directly
transportable to other machines and operating systems. It
responds
instantly, changing the 3D view appropriately when any 2D view is
edited.
3. New Acrylic Sculptures
This
section shows four examples made from laser-cut acrylic plastic, i.e., Plexiglas.
In each case, the completed sculpture is shown at left and a single
component
at right. To make wooden or Plexiglas models, the 2D layout is output
as a
DXF-format geometry file used to cut the shapes. After cutting,
the parts
that mate are mitered so they can butt at the proper dihedral
angle. (The
dihedral angles are output separately by the program. For a metal
sculpture,
these angles are the fold angles, or could be used to set jigs that
hold pieces
in relative position for welding or brazing.) Then the parts are
then
intricately interwoven (which usually took several hours) and glued
with a
solvent cement.
|
|
|
|
Figure 13:. Deep Sea Tango, 15 cm |
Figure 14: One component of Fig. 13 |
Figures
13 shows Deep Sea Tango, which can be thought of as twelve
starfish-like
forms "holding hands" in a complex ballet position. It is
assembled from twelve identical parts, each as in Figure 13, which only
touch each
other at their tips. Because of the transparent material, it is
difficult to
capture in a photograph how the many arms just manage to pass by each
other at
various angles. The design is based on the great dodecahedron,
and
conceptually very similar to Tangled Reindeer, (cf. Figures
10-12) but
twelve rigid parts shaped like Figure 12 could not be assembled because
they
would block each other's movement. These parts (Figure 14) have
much less
branching, but even so, it is just barely possible to assemble them.
|
|
|
|
Figure 15:. Quintessence of Hedgehog, 15 cm |
Figure 16: Two shapes of components for Fig. 15 |
Figure
15 shows Quintessence of Hedgehog, which contains twenty-four
windmill-like
parts, twelve in each of two slightly different 5-fold shapes.
They lie
in the face planes of two concentric parallel dodecahedra. The larger
parts lie
in the planes of the smaller dodecahedron as they have to extend
further to
reach the circumsphere where the two types of parts meet. The
sixty
junction points are each the meeting of one large arm and one small
arm. (The
design program allows the user to create several editor windows, each
like
Figure 12. The intersection lines of each plane with all the other
planes are
color-coded to distinguish the different families. Points on the
lines of
intersection of two families show up in both editors, and if dragged in
one
plane make the corresponding motion in the other plane.)
|
|
|
|
Figure 17:. This End Up, 23 cm |
Figure 18: One component of Fig. 17 |
Figure
17 shows This End Up, which contains twenty parts of the form
shown in
Figure 18, lying in the planes of an icosahedron. The parts pass
around each
other without touching, except for where they are joined at the arrow
tips in
groups of four. The structure is based on the uniform compound of
five
regular octahedra, which is one of the stellations of the icosahedron.
It
took almost two hours for me and ten members of the Stony Brook
University math
club to assemble this. I originally thought that ten people could each
hold two
parts and translate them all together "from infinity" but we couldn't
get the interweaving just right, and we eventually found a less
systematic
assembly method which did work.
Lastly,
Figure 19 shows Bouquet, which contains thirty S-shaped
parts as
shown in Figure 20. The components lie in the face planes of a
rhombic
triacontahedron, but the viewer sees it as a dozen flowers that nestle
inside a
dodecahedron. The ends meet in groups of three, but in the
interior the
components make 5-fold spirals without contacting. Because of the long
thin
parts, this sculpture is slightly flexible.
|
|
|
Figure 19: Bouquet, 23 cm |
Figure 20: One component of Fig. 19 |
4. Conclusions and Future Work
For several years I have been exploring a
space of
forms with symmetrically arranged planar components. [3] I find that
they can
be visually and intellectually engaging, with a rich mix of simplicity,
complexity, geometry, and an organic quality. (In addition, a
practical
benefit of this class of sculpture is in transportation: One can ship
the parts
of a large work as a flat package and assemble them on site.) To
explore further
in this family, I created a design program to virtually prototype new
works. This real-time explorer of spatial ideas allows for more
complexity than my previous sculptures, permitting intertwined
relationships
between several families of planes. It encourages experimentation while
handling the computational issues of maintaining symmetry, planar
intersections, and layout.
As an interactive sculpture design tool, it
was
inspired in part by Sequin's tool for generating sculptures in the
style of
Brent Collins. [4] The program presented here is in some ways
analogous, but
with a different family of forms. There are a number of previous
programs which
allow the user to design stellations, e.g., [1] and [5], but as far as
I know
no previous work allows freeform design in the stellation planes.
This is an ongoing project with many future
directions, mainly additional sculptures. I also have a list of
software
enhancements to add, such as other forms of extrusions, and edge
treatments for
the RP results.
References
[1] V. Bulatov, "An Interactive Creation of Polyhedra Stellations with Various Symmetries," Bridges 2001: Mathematical Connections in Art, Music and Science, Reza Sarhangi (editor), 2001.
[2] H.S.M. Coxeter, P. DuVal, H.T. Flather, and J.F. Petrie, The Fifty-Nine Icosahedra, U. Toronto Pr., 1938, (Springer-Verlag reprint, 1982), (Tarquin reprint, with additional images, 1999).
[3]
G.W. Hart, see list of references at http://www.georgehart.com
[4] C.H. Sequin, "Virtual Prototyping of Scherk-Collins Saddle Rings" Leonardo 30:2, pp. 89-96, 1997.
[5] R. Webb, "Stella: Polyhedron Navigator," Symmetry Culture and Science, 11, No. 1-4, pp. 231-268, 2000/2003.
Acknowledgments: Thank you Jim Quinn for the RP
production, and
Chris Palmer for the laser cutting.
Addendum: For more pictures and info about the acrylic
sculptures, click
here.