Abstract: A method for constructing images of icosahedral geometric structures is described. An example Artificial Radiolarian Reticulum illustrates the process. The algorithm was devised for producing images of sculptures too complex to realize by traditional means. One image is detailed and others are available at the author's web page.

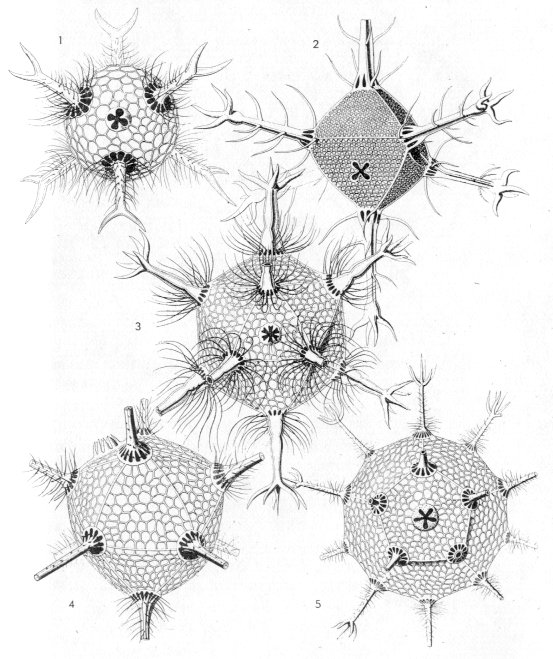
The nineteenth century naturalist Ernst Haeckel explored the globe with an eye for the beauty of natural organisms and created artful drawings of a wide variety of plants and animals. [1] Haekel's drawings of radiolaria—microscopic ocean protozoa—are often reprinted in works dealing with geometry, symmetry, and art. There are a great many radiolarian species, with widely varying forms, but in many the skeleton, or reticulum, is highly perforated and adorned with branching spikes. Hermann Weyl's classic book Symmetry [2] reprints several of Haekel's drawings to illustrate that some radiolaria have the symmetry of Platonic polyhedra. See Figure 1.
 

Fig. 1. Radiolaria skeletons drawn by Ernst Haeckel. Reprinted from [2].

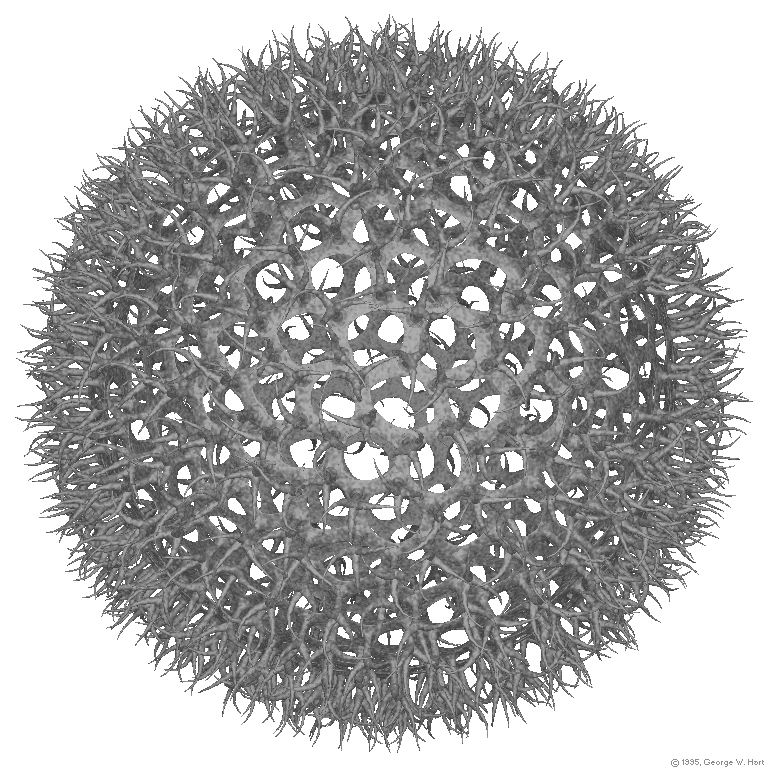
As a sculptor of organic geometrical forms, [3] I have long been entranced by Haekel's artwork and its implications. I create mathematically based sculptures, such as Loopy, shown in Figure 2, but there are limits to the complexity that one can physically attain. So I have created a purely mathematical image of a radiolarian-like nature, which is informed by this mathematical and biological background. My Artificial Radiolarian Reticulum, Figure 3, attempts to capture something of the essence of radiolaria, without being overly representational or true to any particular species.
 

Fig. 2. Loopy, George W. Hart, 1999, painted aluminum.

The rendering was performed in the freely available ray tracer POVRAY, [4] which reads an input text file describing a scene. A POVRAY scene file can contain a wide variety of geometric primitives, e.g., cylinders and cones, which can be combined by standard constructive solid geometry operations, e.g., union, intersection, and linear transformation. In addition, the file specifies materials, textures, lighting, camera position, and other scene properties.
 

The bulk of the scene description for this radiolarian image specifies the union of a large number of cones and cylinders, automatically positioned as described below. A small, hand-tweaked portion of the file sets the scene. To obtain a flat lighting characteristic of photomicrographs, the lights were placed near the camera and shadows were turned off. A distance-proportional gray "fog" was used, to give the distant surfaces lower contrast than the near surface. A dull, white, bumpy texture was specified, for a bone-like feel.

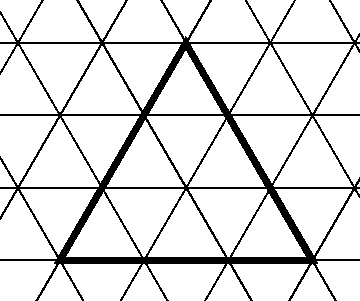
The novel aspect of this process involves a program that positions components into a geodesic sphere. A geodesic sphere is any triangulated structure in which the vertices lie on the surface of a sphere. The program accepts a set of user parameters and outputs a file of POVRAY code that is imported into the scene description. The file is just a long sequence of translated, rotated, scaled instances of user-specified object types. The remainder of this paper describes the workings of the placement algorithm.

The algorithm accesses a table of the xyz coordinates of the vertices of a regular icosahedron (centered at the origin) and divides the faces into smaller triangles to produce the vertices and edges of the geodesic sphere. Figure 4 shows an example of a triangle divided into nine sub-triangles each having one-third the edge length. Dividing each of the 20 triangles of an icosahedron in this pattern and normalizing to unit magnitude gives a triangulated sphere with 180 faces. Because the icosahedron edges are divided into thirds, this is usually called "a frequency three geodesic sphere." The algorithm can produce that, but also allows for the more interesting case of a rotated division in which the triangles of the icosahedron are divided into sub-triangles not parallel to the original edges.
 

Fig. 4. Triangle nine times the grid triangle area.

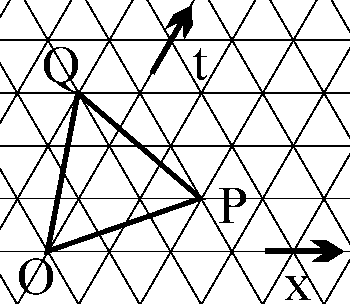
Figure 5 shows a triangular lattice and a "slanted" equilateral triangle OPQ marked with bolder lines. The center of the larger triangle is a 3-fold axis, and the midpoints of its edges are 2-fold axes, of the triangular lattice. So if one places a copy of OPQ on each face of an icosahedron, the lattice lines will continue properly across the icosahedron edges, and the rotational symmetries of the icosahedron are preserved. Generally, specifying any point P of the triangular lattice defines a division for a geodesic sphere. In terms of a t-axis which is 60 degrees counterclockwise of the x-axis, the example shows the simplest chiral case: P is given by x=2 and t=1. As a special case, the type of division in Figure 4 occurs when t=0, so P is on the x-axis. The large and small triangles are orthogonal if t=x, which is common in architectural applications because it preserves both rotational symmetry and mirror symmetry.
 

Fig. 5.  Triangle seven times the grid triangle area.

In Cartesian (x, y) coordinates, we have unit vectors x=(1, 0) and t=(1/2, sqrt[3]/2). Using square brackets for [x, t] coordinates, we choose P=[x, t] and then OPQ is equilateral if Q=[-t, x+t]. The vertex construction process takes the xyz coordinates of O, P, and Q from one face of an icosahedron, and finds the lattice points ix+jt, for integers i and j, on the face. It is straightforward to invert the transformation and find (or just check) that x = ((x+t)/d)P + (-t/d)Q and t=(t/d)P + (x/d)Q, where d= x²+xt+t².

So, given the vertices V₁, V₂, V₃ in counterclockwise order of any face of a regular icosahedron centered at the origin, we can take O= V₁, compute P= V₂-V₃ and Q= V₃-V₁, and find integer lattice points v_ij=ix+jt using the above expressions for x and t. Nested iteration of i and j produce a parallelogram-shaped portion of the lattice, and just the points v_ij interior to OPQ are collected, by standard tests. Doing this for all twenty faces, a list of all vertices is collected. Points on the boundaries of the faces, e.g., on the segment OP, need to be detected and entered only once in the list, again by standard means. As a check, we verify that there are 10d+2 vertices in the complete list. This is because d is the ratio of the area of OPQ to the area of a lattice triangle, so there will be 20d small faces, 30d edges, and by Euler's theorem, 10d+2 vertices.

Given the list of vertices, {v}, the next task is to identify which pairs of vertices are connected by edges. A simple method is to test all pairs and see for which |v_n-v_m|² <= |x|². After this, the vertex coordinates are normalized to unit length, so they lie on a sphere rather than an icosahedron. This distorts the triangles slightly from equilateral. In addition, the algorithm optionally allows that the vertices are each perturbed by a random displacement vector, within a maximum distance specified as a fraction of the lattice edge length.

The algorithm also allows the option of dropping certain classes of vertices or edges. For example, skipping the points where (i-j) mod 3 = 0 leaves out the vertices at the centers of hexagons, resulting in a hexagonal tessellation. Similarly, leaving out the points where i mod 2 = 0 and j mod 2 = 0 results in the tessellation where hexagons and triangles alternate. (In both cases, only certain values of x and t are suitable for the pattern to continue across face boundaries.) Other program options allow omitting the 5-fold vertices, or omitting all points on a given side of a given plane, to produce partial spheres, e.g., hemispheres.

For the radiolarian image, x=t=6, the hexagonal tessellation option was chosen, and vertices were randomly perturbed up to 0.25 times the edge distance. This results in d=108, so the complete triangulated structure would have 1082 vertices and 3240 edges. But dropping the vertices at the centers of the hexagons leaves 362 openings (twelve 5-sided, the rest 6-sided), with 720 vertices, and 1080 edges. When looking at a structure, the first thing a geodesic sphere aficionado usually does is to seek the 5-fold axes, but this is difficult here because of the random perturbations.

Given the coordinates of the vertices and the list of vertex pairs which bound edges, it is a straightforward translation operation to output a set of POV commands which place objects at the vertices and along the edges. Appropriate arctangent operations are used to determine rotations so that the flattened cylinders along the edges are tangent to the sphere and the prongs at the vertices are normal to the sphere. The tendril-like forked prongs are all identical assemblages of cones. They were created by a simple L-system definition [5, 6] outside of this process. The L-system is a language specification for fractal structures, which easily allows multiple levels of branching, as in tree branches. As the radiolarian prongs are not multiply divided in my final design, the L-system approach turned out not to be necessary, but the initial design allowed for the possibility of a higher level of division.

In a final step, as a touch of the artist's hand, a dozen prongs were manually deleted from the file, giving a small "bald spot" to the right of center in the image, allowing a clearer side-on view of the prongs beyond it. This was just done by experiment until a satisfactory result was found.

This same program, with various options selected and sundry values for x and t, was used to generate a variety of images available on the author's web pages. [7] In each case, different POV components were hand-defined for the edges and/or vertices. One image shows an assemblage of paper clips, which is so realistic that some viewers routinely assume it is a photograph and send the author email asking for construction instructions.

References

[1] Haeckel, Ernst, Kunstformen der Natur, 1904. Dover reprint as Artforms in Nature, 1974.
[2] Weyl, Hermann, Symmetry, Princeton, 1952
[3] Hart, George W., Geometric Sculpture, http://www.georgehart.com/sculpture/sculpture.html
[4] The POV team, POVRAY, http://www.povray.com/
[5] Pruskinkiewicz, Przemyslaw and Lindenmayer, Aristid, The Algorithmic Beauty of Plants, New York : Springer-Verlag, c1990.
[6] Lapré, Laurens, L-parser software, http://www.xs4all.nl/~ljlapre/
[7] Hart, George W., Pavilion of Polyhedreality,http://www.georgehart.com/pavilion.html

I recently discovered the following reference, which covers similar material:

H.S.M. Coxeter, "Virus Macromolecules and Geodesic Domes," in A Spectrum of Mathematics, J.C. Butcher (editor), Aukland, 1971.

Michael Goldberg, A Class of Multi-Symmetric Polyhedra, Tohoku Mathematics Journal, 43, 1937,  pp. 104-108.

Magnus J. Wenninger, Spherical Models, Cambridge, 1979 (1999 Dover reprint).