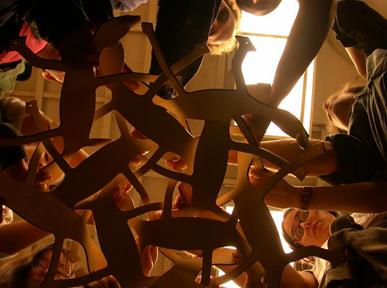This is
a webified version of a paper which
appeared in Bridges 2004
A Salamander Sculpture Barn Raising
George W. Hart
Computer Science Dept.
Stony Brook University
Stony
george@georgehart.com
Abstract
Salamanders is a thirty-piece wooden sculpture that was
group assembled by thirty
volunteers in an exciting sculpture "barn raising"
when I was artist-in-residence at M.I.T. in October/November 2003. It
is
composed of laser-cut salamander-shaped components which lie in the
planes of a
rhombic triacontahedron and were mathematically designed to weave
through each
other and exactly fit together on the outside.
1. Introduction
M.C.
Escher playfully incorporated chameleons and other reptiles or
amphibians in
his two-dimensional geometric artwork [1]. In homage to his creative
spirit, I
designed my sculpture Salamanders to
feature flat salamanders which interweave in three dimensions. Figure 1 shows it hanging temporarily inside
a window overlooking the construction of Frank O. Gehry’s
new
|
|
|
Figure 1: Salamanders |
My ultimate concept, if funding can be found,
is for
a large metal double sphere as shown in Figure 2. The inner and outer
spheres
are each made of thirty identical two-headed salamander shapes. Each
part is
parallel to an identical part similarly oriented in the other sphere. I
find it
visually interesting to show that the same salamander parts can be
joined in
these two contrasting arrangements---one very open and one very
interlocked. It
is a puzzle with two very different solutions.
The outer sphere of Figure 2 does not present
any
inordinate construction challenges. I am certain that I can fabricate
its
thirty components and assemble them. The inner sphere was my
fundamental
concern. From a computer rendering such
as Figure 3, I can verify that there exists a configuration in which
the parts
do not intersect each other in the interior, yet exactly meet
edge-to-edge
along the exterior. However there is no
mathematical method to determine if the thirty initially separate rigid
components of this sculpture can be physically manipulated to weave
them into
the desired configuration. What is the assembly algorithm? Notice that
one
could not simply position pieces one at a time, because if one tried to
insert
the last piece after all the others are positioned, the legs would
block
access.
The two hands of one sculptor are not sufficient to manipulate so many components simultaneously, so this was an ideal question for the collective creativity of a group assembly project. I have led other sculpture “barn raisings” [4], but for them I had a proven assembly algorithm pre-designed. When I was invited to be artist in residence at MIT [6], this thirty-component assembly project struck me as an ideal group activity to try there.
|
|
|
|
Figure 2: Salamanders, concentric spheres
concept. |
Figure 3: Inner sphere of Figure 2. |
2. Design
Although geometric and salamander-filled, in most ways this work involves very different design problems than Escher’s art, because these parts interweave in three dimensions. Both spheres of Figure 2 fall within a large family of geometric sculptures I have been exploring [5], based on symmetrically arranged planar components. Physically, these works consist of interwoven identical components that can be accurately laser cut, delivered flat to the assembly site, then woven through each other on-site and fastened together. Mathematically, the design of these sculptures involves drawing within the “stellation diagrams” of polyhedra. Other software exists for creating stellated polyhedra [9], but my approach [5] is unique in allowing design and visualization of free-form drawings within the stellation planes. Stylistically, this allows me to create an Escher-like sense of structured confusion.
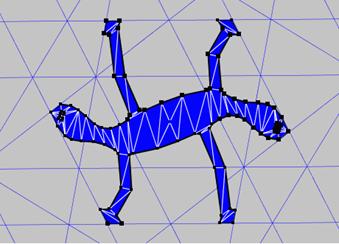
For Salamanders, the underlying polyhedron is the rhombic triacontahedron (RT), which consists of thirty “golden rhombi,” arranged with icosahedral symmetry, as shown in Figure 4. When the thirty face planes of the RT are extended to infinity, the pattern of their intersection in any one of the planes is a set of lines partly visible in Figure 5. Superimposed over these lines is the shape I drew for the salamander part. The dark lines are to be laser cut and the light inner lines indicate how the area is divided into triangles.
|
|
|
|
Figure 4: Rhombic triacontahedron (30 rhombi) |
Figure 5: Salamander layout in RT stellation diagram |
If made in metal plate, I would design tabs with
holes
attached to the feet, folded to the proper dihedral angle. Dotted lines
in
Figure 6 show how two foot tabs could connect on the back of the head.
Round-head bolts with hexagonal sockets would be used to hold
everything
together and also serve as eyes. However, for joining the wood
components, I
pre-made sixty small wood connectors, miter-cut at the appropriate face
angles
and dihedral angles. The feet screw into a connector glued behind each
head.
|
|
|
|
Figure 6: Design with bolts for eyes |
Figure 7: Solid freeform fabrication model |
A 3D model of the form is shown in Figure 7. It is a 2.5 inch diameter model made on a Stratasys/Objet Eden 333 machine. The .stl file that describes its geometry is available at my web site for anyone with solid freeform fabrication equipment who wishes to make a copy [3]. Such models are assembled in thin cross-sectional layers on a 3D printing machine, so they give a visual and tactile sense of the structure. But they do not demonstrate whether the form could be assembled from rigid planar components.
I was afraid to put myself in the embarrassing position of creating thirty large parts and bringing a crew of thirty people together only to find out my design was impossible to assemble. So I made a seven-inch prototype in rigid acrylic plastic (Plexiglas), to verify that the parts can be woven without jamming together. Before I had thirty four parts cut, I had to lay them out for the 24 inch square working area of a laser cutting service. Interestingly, the parts pack together quite tightly, minimizing material wastage, as seen in Figure 8.
It took half a day to assemble the plastic
parts. By wiggling
parts slightly to open small spaces which let other parts be inserted,
all the
while holding everything loosely together with many fingers, bits of
tape, and
small rubber bands, eventually I managed to get the last piece in place. So I had an existence proof that assembly was
possible, but I certainly did not have anything like a well-defined
assembly
algorithm. The resulting model, after gluing the parts, is shown in
Figure 9.
Because it is clear, it may difficult to determine what is what in that
photo,
but I can attest that in person it is quite cool looking.
|
|
|
|
Figure 8: Layout for laser cutting
plastic parts |
Figure 9: Plexiglas model, 7 inches |
3. Sculpture Barn Raising
When the time came
for my
residency at MIT, I brought the acrylic model and the 3D printing model
with me
to show people what we would be building at the group assembly event. I
am very
grateful to my host Erik Demaine, and also
to Marty Demaine and Abhi
Shelat, all of whom spent many hours with
me on the
preparations. In the days there before the assembly, we used a laser
cutter to
cut the thirty wood salamanders (and some spares). The wood we finally
selected
is a Baltic birch plywood, laser-engraved
with ovals
for the eyes, then sanded, drilled and countersunk in four places for
screws,
glued to two mitered wood junction pieces, and given a protective
coating of
tung oil. We also made a large quantity of scaled-down paper
salamanders for
practice assembly. One important lesson we learned late along the way
is not to
purchase large amounts of expensive ash plywood of a type which chars
into
embers when one tries to laser-cut it.
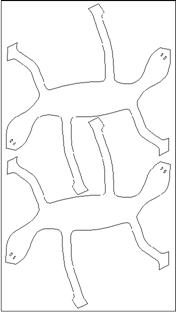
If you want to make your own paper or wood model, Figure 10 is an image of how we laid out a pair of parts in the 32-by-18 inch bed of the laser cutter we used. Even without a laser-cutter, you can make thirty copies (enlarged) on card stock, cut them out with scissors, and assemble your own paper model.
|
|
|
|
Figure 10: Layout for cutting wooden parts |
Figure 11: Taped together paper model |
On the day of assembly, roughly fifty volunteers
started
work around four large tables in one of the studio art rooms. Everyone
received
an envelope with thirty laser-cut paper salamanders. After some
instruction on
how the parts go together, and by studying the models I brought, we
began
individually or in small groups to assemble. Figure 11 shows one of the
paper models.
Figure 12 shows its construction. Small pieces of clear tape hold a
long leg, a
short leg, and a head at each of the sixty junctions. It is important
to
understand that the two-headed salamanders can have their heads all
facing to
the left or all facing to the right, and that each salamander is part
of two
different types of pentagonal cycles.
|
|
|
Figure 12: Working on the paper models |
It is initially tricky to master how the parts
weave
through each other, and internalize what should be inside and what
should be
outside. The long legs which make a star pattern at the five-fold
junctions are
the biggest problem. The "ankle" of each long leg must be outside of
the "knee" of the leg it crosses. Paper is flexible, allowing legs to
be bent around each other and into place. But the real challenge for
everyone
was to design an assembly strategy which would later work with rigid
wooden
components. After an hour and fifteen minutes of paper practice, I felt
that
enough people understood the structure. We then started on the real
assembly of
the wooden parts.
|
|
|
Figure 13: Starting the assembly of the wooden salamanders |
|
|
|
Figure 14: Looking up into the first cap
of ten salamanders. |
After some discussion, the assembly method we
chose was
based on three units of ten salamanders each: two polar caps and an
equator.
Figure 13 shows the initial step, working in the air with five parts
around an
imagined vertical five-fold symmetry axis. Then another five parts
weave into
those, making the first cap of ten parts. Figure 14 is a view from
below
looking up into the first cap being assembled. It was loosely screwed
together,
and then put aside. A second cap was assembled in the same manner. Our
strategy
was to make an equator of the remaining ten parts to connect the top
and bottom
caps.
|
|
|
|
Figure 15: Adding the equator to the
bottom ring. |
Figure 16: Finishing the equator |
We did the final assembly by placing one cap facing up on the table and first adding an equatorial ring of five salamanders whose bodies are aligned vertically, as seen in Figure 15. Then we wove in the overlapping equatorial ring of five salamanders whose bodies are aligned more horizontally, shown in Figure 16. (Each salamander is part of one ring of each type; each five-fold equator is made of both types of ring, concentrically arranged but not contacting each other.) Finally, the other cap was lowered on to the top, as shown in Figure 17. This last step took some time and a number of retries to get the legs properly interwoven.
|
|
|
Figure 17: Adding the top cap |
Everything worked out, so the
remaining screws could be
inserted and all 120 screws were tightened. The final result is in
Figure 18. I
found it to be surprisingly rigid for its 15 pounds of weight. The
total time
for the assembly of the wooden parts was one hour and forty minutes.
|
|
|
Figure 18: Finished! |
4. Conclusion
I consider the Salamanders barn raising to have been a great success. I am very happy with the final sculpture and the wonderful preparation and assembly support that I received at MIT. Many more photos plus short digitized videos of the assembly are available online [7]. The work has been selected as the first in the art collection of the MIT Computer Science and Artificial Intelligence Laboratory. Our plan for its future is that it will hang in the new Stata center. After it is moved to its public location, I hope Salamanders will remind viewers of the beauty of geometry and the tradition of M.C. Escher.
References
[1] M.C.
Escher, Bruno Ernst, The Magic
Mirror of
M.C. Escher, Ballantine, 1976.
[2] Frank
O. Gehry,
[3] George
W. Hart, web pages, http://www.georgehart.com
[4] G.
Hart, "The Millennium Bookball," Proceedings of Bridges 2000:
Mathematical
Connections in Art, Music and Science, Southwestern College,
[5] G.
Hart, "Sculpture from Symmetrically Arranged Planar
Components", in Meeting Alhambra, (Proceedings of ISAMA-Bridges 2003,
Granada, Spain), Javier Barrallo et al
editors, Univ.
of Granada, 2003, pp. 315-322.
[6] MIT
artist-in-residence program, http://web.mit.edu/arts/special_programs/air/index.html
[7] MIT
page of
photos and videos, http://theory.lcs.mit.edu/GeorgeHart/residence_101103.htm
[8] MIT
Tech
Talk articles, http://web.mit.edu/newsoffice/tt/2003/nov19/salamander.html
[9] R. Webb, "Stella: Polyhedron Navigator," Symmetry
Culture and Science, 11, No. 1-4, pp. 231-268, 2000/2003.
Acknowledgments
I
thank the many people at MIT who made this project possible. First and
foremost,
Erik Demaine invited me to be
artist-in-residence
through the Office for the Arts and the EECS department. Erik Demaine, Marty Demaine,
and Abhi Shelat
spent many hours with
me doing the preparations, especially laser-cutting the wood and paper.
Rebecca
Frankel helped with the oil finish. The CSAIL fabrication shop and
staff
provided the laser-cutter and other resources. Erik Demaine,
Mark Hoffman, and Moses Liskov took many
photos,
including the ones in this paper. Tom Buehler from the CSAIL Computer
Graphics
group took and edited video. Michele Oshima,
Nicole
Ackerman, and Marc Rios at the MIT office for the Arts did
advertisement and
behind-the-scenes logistic arrangements. Tech Talk ran nice articles
which
helped draw a crowd to the event and report the results [8]. And of
course, my
thanks most of all go to each of the barn raisers who came and
participated in
the assembly.