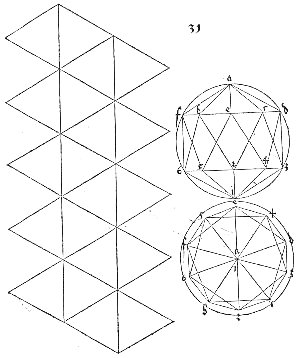
Durer's Polyhedra

    Albrecht Durer, the remarkable German renaissance printmaker (1471-1528), made an important contribution to the polyhedral literature in his 1525 book, Underweysung der Messung, available in English translation as Painter's Manual. It was one of the first books to teach the methods of perspective, and was highly regarded throughout the sixteenth century.  Durer travelled to Italy to learn perspective and wanted to publish the methods so they were not kept secret among a few artists.  Who he learned from is not known, but Luca Pacioli is a likely possibility.  Some of the techniques and illustrations follow very closely the work of Piero della Francesca.

    Durer's Underweysung der Messung contains a very interesting discussion of perspective and other techniques and it typifies the renaissance idea that polyhedra are models worthy of an artist's attention. More importantly, this book presents early examples of polyhedral nets, i.e., polyheda unfolded to lie flat for printing. The image at right is Durer's drawing of the net of an icosahedron. While the net is correct, his techniques of perspective were still under development, and it is interesting to observe that the projection at the upper right has a number of inaccuracies.
     
     
     

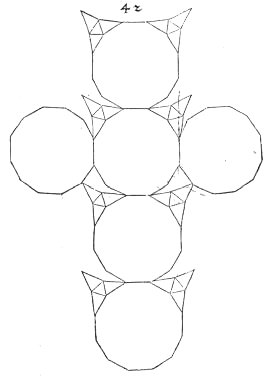    Here is another of Durer's nets. This is intended as a truncation of a truncated cube. While most of his nets are quite accurate, this contains a significant error, which you will notice if you study it for a few moments. Eight of the vertices (those at the top left and top right of the four central dodecagons) show 360 degrees worth of angles around them, and so can not fold as intended. This should serve as a reminder that the idea of a net is not as simple and obvious as one might suppose.

    An interesting property of this polyhedron, which might be why Durer included it, is this: if the dodecagons are regular then it can be inscribed in a sphere.


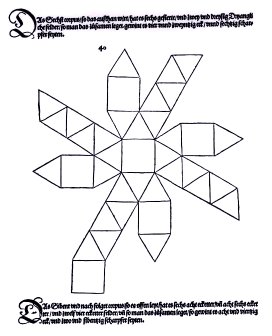    The Underweysung der Messung is also significant because it contains the first presenation of the snub cube. The snub cube is the first of the chiral Archimedean solids to be rediscovered in the Renaissance.  (The other, the snub dodecahedron, had to wait for Kepler.)  Given the chirality of the snub cube, it strikes me as strange that Durer did not give a picture of the solid itself or mention its two forms.  He contented himself with the net at right.


    One of Durer's masterpieces, the engraving Melancholia I, features a frustrated thinker sitting by an uncommon polyhedron. (Click the image for a larger version.) Much has been written analyzing the symbolism in the image and the possible meaning of every element including the polyhedron. One might speculate that the cube represents masculinity and truncating one in an upright position may have some Freudean symbolism.

    Geometrically, the polyhedron is simply a cube or rhombohedron which has been truncated at the upper vertex. (I can not decide if the lower vertex is also truncated so the solid rests on a triangular face, or if the lower vertex symbolically penetrates the earth, but no other writers seem to allow for that possibility.) Panofsky accurately describes it simply as a "truncated rhomboid."  It is possible to proportion it so that the vertices project onto a 4-by-4 square grid like that of the magic square (see the papers by Lynch and Sharp).  Schreiber proposes that it comes from a rhombohedron with 72-degree face angles, which has been truncated so it can be inscribed in a sphere. This polyhedron continues to sire a considerable literature, so for those who wish to read some of what has been written about it, here are a few references to get you started:

    • P. J. Federico, "The Melancholy Octahedron," Mathematics Magazine, pp. 30-36, 1972.
    • T. Lynch, "The geometric body in Durer's engraving Melancholia I," Journal of the Warburg and Courtauld Inst., pp. 226-232, 1982.
    • C. H. MacGillavry, "The Polyhedron in A. Durer's 'Melancolia I': An Over 450 Years Old Puzzle Solved ?" Netherland Akad Wetensch. Proc., 1981.
    • E. Panofsky, The Life and Art of Albrecht Durer, Princeton, 1955.
    • P. Schreiber, "A New Hypothesis on Durer's Enigmatic Polyhedron in His Copper Engraving 'Melencholia I'," Historia Mathematica, 26, pp. 369-377, 1999.
    • K. D. Walton, "Albrecht Durer's Renaissance Connections Between Mathematics and Art," The Mathematics Teacher, pp. 278-282, 1994.
    • J. Sharp, "Durer's Melancholy Octahedron," Mathematics in School, Sept. 1994, pp. 18-20.
    Virtual Polyhedra, (c) 1997,George W. Hart