Luca Pacioli (1445 - 1514, sometimes "Paciolo") is the central figure in this painting (by Jacopo de Barbari*, 1495). Perhaps no other work so epitomizes the deep Renaissance connection between art and mathematics. Pacioli (a Franciscan friar, shown in his robes) stands at a table filled with geometrical tools (slate, chalk, compass, dodecahedron model, etc.), illustrating a theorem from Euclid, while examining a beautiful glass rhombicuboctahedron half-filled with water.
Every aspect of the picture has been composed meaningfully, and art historians have analyzed it at length, yet the figure at right remains a mystery. For two rather different conclusions, see the references by M. Davis (who suspects the figure is a self-portrait of the painter) and N. MacKinnon (who proposes that the figure is Albrecht Durer---compare Durer's 1498 self-portrait).
The
polyhedron in the painting is a masterpiece of reflection, refraction,
and perspective. (Davis states that the bright region on its surface
reflects
a view out an open window, showing the Palazzo Ducale in Urbino.)
Certainly an actual glass polyhedron was used as a model. (Pacioli
states
in his books that he constructed several sets of glass polyhedra, but I
know of no other information about them.) The polyhedron in the
painting
is beautifully positioned, suspended with a 3-fold axis vertical, out
of
physical contact with the other objects in the scene. I suspect
that
Pacioli chose it for the portrait because he discovered this form and
was
quite proud of it. (Presumably Archimedes first discovered it,
but
that wasn't known in Pacioli's time.) The painting is the
earliest
known image of the rhombicuboctahedron.
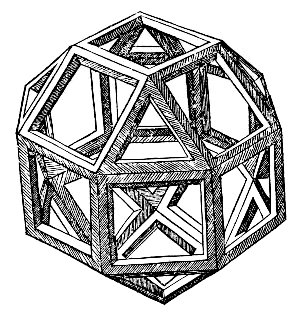
At right is shown the first printed illustration of that polyhedron, which appeared in Pacioli's 1509 book, De Divina Proportione. (He coined the term "the divine proportion" for what is otherwise known as "the golden ratio".) The illustrations were drawn for Pacioli by his friend Leonaro da Vinci. The book was very influential in circulating information about geometry, and polyhedra in particular. Unfortunately, it appears that Pacioli plagarized parts from unpublished manuscripts of Piero della Francesca, whose mathematical accomplishments thereby remained uncredited until the manuscripts were rediscovered in the early 20th century.
Leonardo's illustrations of wooden models were especially influential, e.g., they appear in spectacular intarsia. (The book also contains the first illustration of the icosidodecahedron.)
There is an entry in the accounts for the building of the Council
Hall
in Florence which indicates that a set of Pacioli's wooden models was
purchased
by the City of Florence for public display. See C. Pedretti,
Leonardo:
A Study in Chronology and Time, (1977), who notes "The official
commission
can only be interpreted as a reference to the symbolism of geometry in
state government as postulated in Plato's Republic."
For a sympathetic biography, see R. Emmett Taylor, No Royal Road:
Luca Pacioli and his Times, 1942 (Arno reprint, 1980). Taylor
presents
an argument that Pacioli's apparent plagarism of Piero's work is not
what
it seems.
* The artist is mis-identified in some references as "Jaco. Bar." who was once thought to be a different artist than Jacopo de Barbari. That error was corrected by Creighton Gilbert, "When Did a Man in the Renaissance Grow Old?", Studies in the Renaissance, Vol. 14, (1967), pp. 7-32.