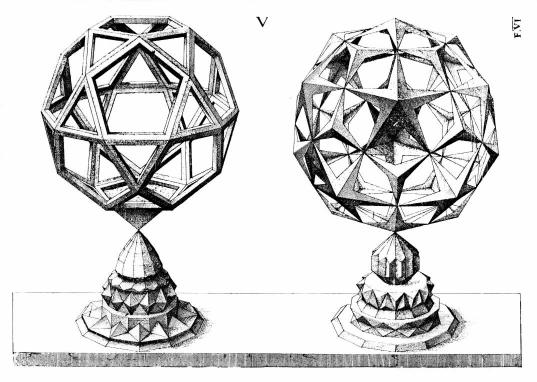
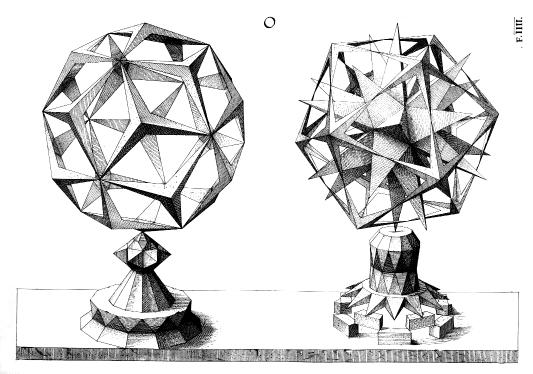
These small reproductions do not show the details of the engravings. Click on this image for a clearer, larger image. The above plate is quite remarkable because the form on the left is almost exactly that of the rhombic triacontahedron, and the core of the shape on the right is almost exactly the great stellated dodecahedron. Both of these were first presented mathematically by Kepler, fifty years later, in 1619.
The other type of plate in Jamnitzer's book is a series of solid forms based on the Platonic solids. A typical one is the following:
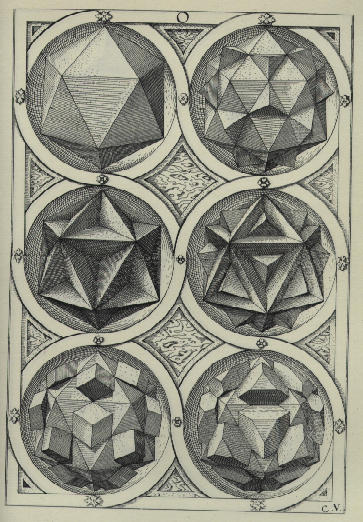
The middle left-hand figure is an anticipation of the great dodecahedron---a nonconvex construction of 12 pentagons---which is usually credited to Louis Poinsot in 1809. The upper right-hand figure is very close to the compound of the icosahedron and dodecahedron. Again, the small size of this reproduction does not allow one to fully appreciate it.
Click here for another of Jamnitzer's plates, but in larger size. It is a series of variations on the dodecahedron. The middle left-hand figure is the rhombicosidodecahedron. (It is first presented, almost simultaneously, both here and in a work of Barbaro.) The middle right-hand figure is an expansion of the icosidodecahedron, similar to this.
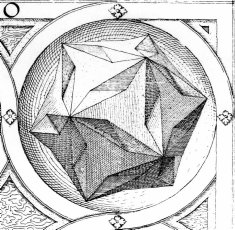Although
there are many interesting images which could be shown here, one in particular
is highly notable. The illustration at right is the only one which
is chiral. It is, perhaps, the first chiral icosahedral object to
be seen since Archimedes' snub dodecahedron.
(The snub cube is presented in Durer's Painter's
Manual some fifty years before this time, but only as a net.
Nothing with chiral octahedral symetry is to be found in Jamnitzer's book.)
To come up with a form representing a new symmetry group is actually a
major mathematical accomplishment by Jamnitzer.
All this artwork is actually a collaborative effort. The engraving
of these images was executed by Jost Amman (1539-1591), but based on drawings
by Jamnitzer. Credit for the imaginative geometric designs goes to
Jamnitzer.